本文解题思维部分主要学习自“极客时间”的《算法面试通关40讲》专栏,加上了我一些自己的见解
动态规划解题思维
- 递归 + (递归中重复计算的部分)记忆化 = 递推
- 对状态的定义,比如
dp[n]中的n代表的内容是什么,有时候根据题目还可能会用二维数组等,如dp[i,j] - 状态转移方程 指的是当前状态与前一个阶段状态的关系,如
dp[n]=dp[n-1] + dp[n-2],类似于递推公式。在一些题型中还可能会涉及if-else判断 - 最优子结构指的是题目符合可以将问题分解为反复求解 前一个最优状态 + 当前状态 即可最终求出最优结果的一个结构
回溯 VS 贪心 VS DP
- 回溯(递归) —— 存在重复计算 (当遇到不存在最优子结构的问题中,我们无法使用动态规划进行优化时,就只能使用回溯穷举所有可能)
- 贪心 —— 永远得到局部最优,贪心算法只顾眼前利益,不管后期的规划,在很多实际问题中应用较少。除非问题每次贪心能最终推得最优解。
- DP —— 在回溯(递归)的基础上,通过记录局部最优子结构的值,减少重复计算
解题思维展示
- 例题:林俊贤从起点走到终点,一次只能向下/右走一步,有多少种走法?(涂了粉色的格子不能走)
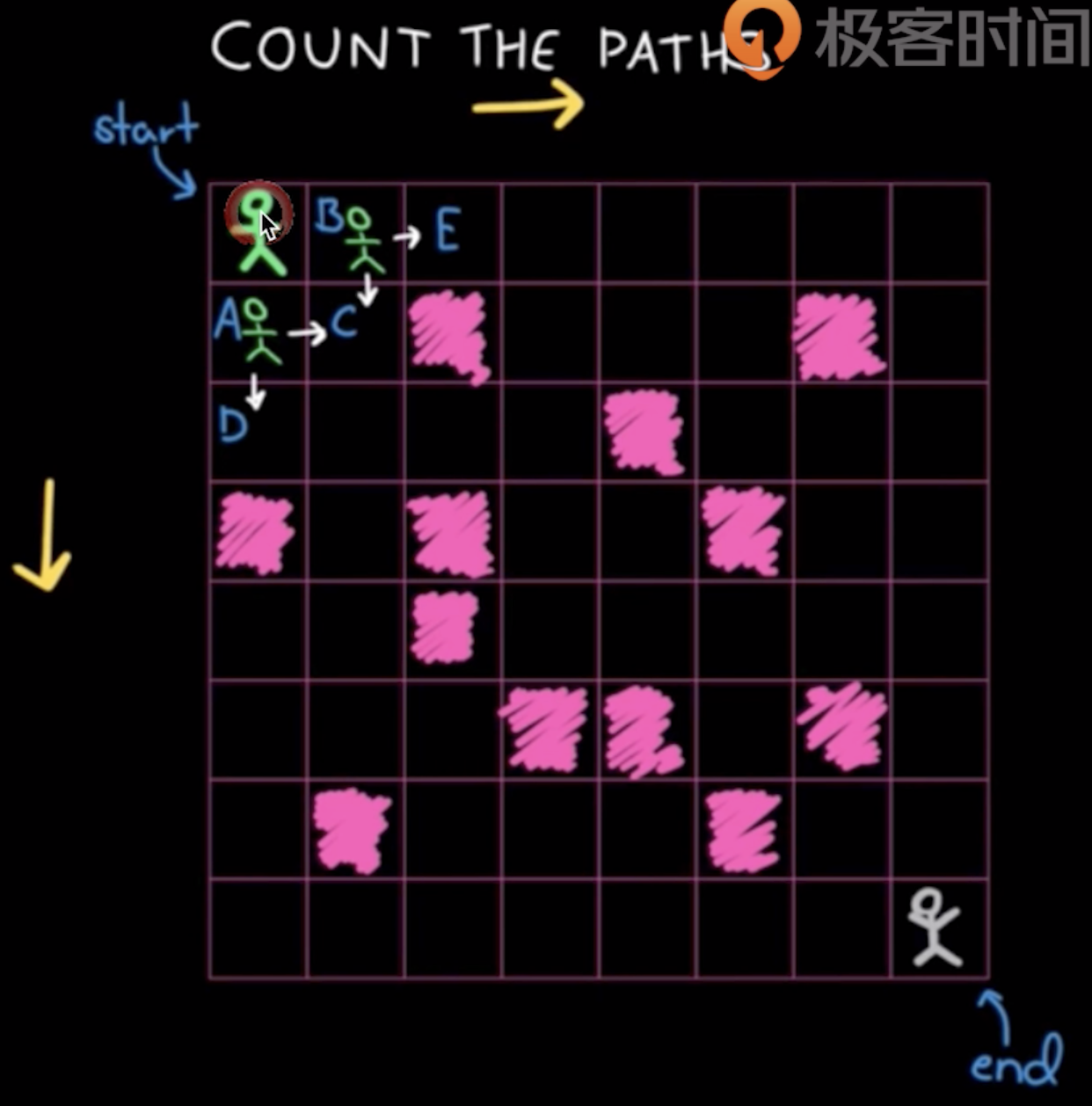
一、递归(但是会存在大量重复运算)—— 思维一般是从上往下/从前往后运行
1 | function countPaths(grid,row,col){ |
二、DP 进行 优化,通过记录避免重复计算 —— 思维一般是从下往上/从后往前运行
对状态的定义,使用
dp[i,j]这样的二维数组来存储当前的最优解状态转移方程
dp[i,j] = dp[i-1,j] + dp[i,j-1]1
2
3
4
5if(grid[i,j]=='空地'){
dp[i,j] = dp[i-1,j] + dp[i,j-1]
}else{
dp[i,j] = 0
}最优子结构 本题很容易看出具有最优子结构,也就是说当前位置的最优解取决于下方节点与右侧节点的最优解,下方节点与右侧节点同理,最终是取决于终点
初始状态 在grid的最下方一行和最右侧一行,由于都只能向右/向下走,所以都是只有一种走法
动态规划经典问题
一、最长公共子序列
- 思路:首先定义状态
dp[i][j]为字符串a1,a2…ai与字符串 b1,b2…bj的最长公共子序列的长度,经过分析可以得到相应的三条公式,具体的我这里就不赘述了,网上有许多关于这个问题的讲解,这里就贴一下我用Javascript实现的代码。
1 | let a = 'xyxxzxyzxy' |
二、01背包问题(指的是背包不可包含一个以上同类物品)
- 思路:
dp[i,j]指的是在j容量下,前i个物品所能得到的最大价值
1 | // capacity |
螺旋KO动态规划习题拳击赛
一、最大子数组
解法对应于Leetcode 53 Maximum SubArray
- 思路:首先找状态转移方程,容易知道有
nums[i] = Math.max(nums[i], nums[i - 1] + nums[i]),一个for循环,数组的位置就存储了对应下标位置可以有的最大子数组的值。但是题目需要我们返回的是最大值,所以我们需要一个额外的变量max来存储当前的最大值
1 | /** |
二、乘积最大子数组
解法对应于Leetcode 152 Maximum Product SubArray
- 思路:此题解法乍一看与上一题类似,很容易想到
dp[i] = Math.max(nums[i],dp[i-1] * nums[i]),但是在实际操作的时候会发现当遇到的nums[i]为负时处理逻辑是不同的,需要分正负两种情况来作讨论,所以我们原先定的一维数组的状态定义是思考不周到的,所以我们加多一个维度,0和1各自代表正负来作区分,形成一个二维数组。之后就是与动态规划一样,for循环,然后比较,最终取正数数组中的最大值即可。
1 | /** |
三、三角形的最小路径和
解法对应于Leetcode 120 Triangle
解法一、常规解法
- 思路:由题意可知,本题应是由三角形的下部开始往上进行动态规划,可列出状态转移方程
triangle[i][j] += Math.min(triangle[i + 1][j], triangle[i + 1][j + 1]),之后根据三角形的特征,使用两个for循环,计算完毕,答案就在三角形的最顶端了,返回triangle[0][0]即可。
1 | /** |
解法二、对常规解法进行优化(状态压缩)
- 思路:与解法一的区别是此处是用一个一维数组就能使得动态规划进行,在此题中它的优势还不算明显,因为本体是可以在triangle原地计算的,在其他动态规划题型中有时候需要new一个二维数组出来辅佐动态规划,但如果我们能灵活地使用状态压缩,用一维数组就做了二维数组做的事,就能较好地降低空间复杂度。
1 | /** |
四、最长上升子序列
解法对应于Leetcode 300 Longest Increasing Subsequence
- 思路:首先处理dp数组的初始状态,即序列只有自己时,均为1。经过分析可以知道
dp[i] = Math.max(dp[i], dp[j] + 1),其中i是外层循环,即遍历nums数组中的每一个数,j为内层循环,指向i前的每一个数,每个dp[i]状态指的是处理至当前i时,最长的上升子序列长度。判断nums[j]<nums[i]如果i前面的数小于它,那么就会比较,是当前位置的子序列长度大,还是前一个状态的子序列(j会走过i前面的每一个数)+1要大。同时外层循环每遍历完一个数,要记得更新res。
1 | /** |
五、硬币最少找零问题
解法对应于Leetcode 322 Coin Change
- 思路:注意dp数组的初始状态,由于状态转移方程我们是求硬币的最少值
min,同时求解过程中还会存在无解的情况,所以我们初始化数组为amount+1,在return的时候就判断dp[amount] > amount ? -1 : dp[amount]。
1 | /** |
面试中的动态规划问题
微信小程序团队一共有 n 名成员,决定出去秋游,在海边遇到出租摩托艇的杰克马,马先生手上有 m 辆待出租的摩托艇,价格分别是 b1 、b2 … bm;
由于习惯了微信支付,团队中每个人身上的现金都有限,分别是 a1 a2 … an,对了,一起出门的老板还带有 S 元的团队经费,这个经费是每个人都可以使用的
那么考虑以下两个场景
场景1
团队成员都很有爱,都愿意借钱给其他同事,那么这时候团队最多能租到多少摩托艇
2
3
return num
}
场景2
团队成员都十分小气,是不愿意借钱给别人的,那么请考虑以下两个问题
//问题一 老板是否能想到一个策略,使得所有人都能租到摩托艇?
2
3
return bool
}
//问题二 请问给出一个策略
// 使得整个团队租到最多的摩托艇
// 在租到最多摩托艇的情况下,整体的支出尽量的少
2
3
4
5
6
return {
num,// 多少摩托艇
cost // 总体资金支出
}
}
调试代码部分
1 | // 一共5人,有7辆摩托 |
1 | // 场景2 问题一 |
场景2的问题二暂时还不会做,有无大神指教一下?
1 | // 场景2 问题二 |